今回からは、先日受験した令和6年度秋期試験の午前Ⅰ共通問題の解説を行っていきます。午前Ⅰの共通問題は、下記試験と共通の問題です。
- プロジェクトマネージャ試験
- データベーススペシャリスト試験
- エンベデッドシステムスペシャリスト試験
- システム監査技術者試験
- 情報処理安全確保支援士試験
今回解説するのは、問1〜5です。これらの問題で使用されていた用語は、以下の5つです。
- AIにおける教師あり学習での交差検証
- 逆ポーランド表記法
- ハッシュ関数
- 実行メモリアクセス時間
- Webアプリケーションサーバの信頼性
是非、最後までご覧いただけると嬉しいです。
AIにおける教師あり学習での交差検証
AI における教師あり学習での交差検証に関する記述はどれか。
ア 過学習を防ぐために、回帰モデルに複雑さを表すペナルティ項を加え、訓練データへ過剰に適合しないようにモデルを調整する。
イ 学習の制度を高めるために、複数の異なるアルゴリズムのモデルで学習し、学習の結果は組み合わせて評価する。
ウ 学習モデルの汎化性能を高めるために、単一のモデルで関連する複数の課題を学習することによって、課題間に共通する要因を獲得する。
エ 学習モデルの汎化性能を評価するために、データを複数のグループに分割し、一部を学習に残りを評価に使い、順にグループを入れ替えて学習と評価を繰り返す。
引用:情報処理安全確保支援士試験 令和6年 秋 午前Ⅰ問1
解答
エ
各解答の手法
ア:正則化
イ:アンサンブル学習
ウ:タスクマルチ学習
エ:交差検証
各解答の解説
AIにおける教師あり学習では、モデルが入力データとその対応する正解ラベルを基に学習しますが、これを改善するための手法として、正則化、アンサンブル学習、タスクマルチ学習、交差検証といった手法が活用されます。それぞれの説明は以下の通りです。
1. 正則化(Regularization)
正則化は、過学習(オーバーフィッティング)を防ぐためにモデルにペナルティを加える技術です。過学習は、モデルが訓練データに過度に適応し、未知のデータに対する汎化能力が低くなる現象です。正則化を行うことで、モデルの複雑さを抑え、汎化性能を向上させます。
- L1正則化(Lasso):モデルの重みの絶対値の合計にペナルティを加えることで、不要な特徴量の重みをゼロにし、特徴選択の効果も期待できます。
- L2正則化(Ridge):モデルの重みの二乗和にペナルティを加え、過度に大きな重みを抑える効果があります。
- Elastic Net:L1とL2を組み合わせた正則化手法。
2. アンサンブル学習(Ensemble Learning)
アンサンブル学習は、複数のモデルを組み合わせることで、個々のモデルの性能を補完し、全体の予測精度を向上させる手法です。アンサンブル学習は、異なるモデルが異なる誤差を補い合うことで、より正確な予測が可能になります。
- バギング(Bagging):同じ種類のモデルを用い、訓練データのサブセットでそれぞれのモデルを学習させ、その予測結果を平均または多数決で統合する手法。代表例はランダムフォレストです。
- ブースティング(Boosting):弱いモデル(通常は精度の低いモデル)を逐次的に学習させ、誤りを修正しながら強力なモデルを構築する手法。代表例はXGBoostやAdaBoostです。
- スタッキング(Stacking):複数のモデルの予測結果を入力として、新たなメタモデルを学習させて最終的な予測を行う手法です。
3. タスクマルチ学習(Multi-task Learning)
タスクマルチ学習は、関連する複数のタスクを同時に学習する手法です。複数のタスクが共有する知識を活用し、各タスクの性能を向上させることができます。異なるタスク間で共通の特徴量や学習した表現を共有することで、モデルの汎化性能を高め、データ効率を向上させます。
- ハード共有:ニューラルネットワークなどのモデルにおいて、最初のいくつかの層をすべてのタスクで共有し、後続の層でタスクごとに異なる部分を持たせる手法。
- ソフト共有:各タスクに専用のモデルを持たせるが、重みの更新時に他のタスクの重みを参照し、学習を進める手法。
4. 交差検証(Cross-validation)
交差検証は、モデルの汎化性能を評価するために、データを複数の部分に分割し、異なるデータで訓練と評価を繰り返す手法です。これにより、データセット全体を有効に使ってモデルの性能を検証できます。
- K分割交差検証(K-fold cross-validation):データをK個の等しい部分に分割し、K回の学習・評価を行う手法。各回で異なる1つの部分を評価用データとし、残りを訓練用に使用する。最終的な性能はK回の評価結果の平均を取ります。
- Leave-One-Out交差検証(LOO):データの各サンプルを一つだけ取り出し、それ以外を訓練用に使う方法。データ数が多い場合、計算コストが高くなります。
これらの手法を組み合わせることで、モデルの性能向上や信頼性の高い評価が可能となります。
逆ポーランド表記法
式 A+B×C の逆ポーランド表記法による表現として、適切なものはどれか。
ア +×CBA
イ ×+ABC
ウ ABC×+
エ CBA+×
引用:情報処理安全確保支援士試験 令和6年 秋 午前Ⅰ問2
解答
ウ
問題の解説
式「A + B × C」の逆ポーランド表記法を求めるためには、演算子の優先順位を考慮する必要があります。通常の中置記法では、乗算(×)が加算(+)よりも優先されるため、まず「B × C」を計算し、その結果に「A」を加える手順となります。
手順:
- 「B × C」は優先されるため、これを先に処理して「BC×」となります。
- 次に「A + (B × C)」を加算しますので、「A」を最初に置き、加算演算子「+」を最後に置きます。
したがって、A + B × Cの逆ポーランド表記は「ABC×+」となります。
選択肢:
- ア +×CBA
- イ ×+ABC
- ウ ABC×+
- エ CBA+×
この中で正しい逆ポーランド表記はウ:ABC×+です。
逆ポーランド表記法
逆ポーランド表記法(Reverse Polish Notation、RPN)は、演算式を記述するための方法の一つで、演算子をオペランドの後ろに置く表記法です。オペランドとは、計算や操作の対象となるデータや値のことをいいます。逆ポーランド表記法は、カッコを使用せずに数式を表現でき、計算を行う際のアルゴリズムが単純になるため、コンピュータでの計算処理に適しています。
基本的な特徴
- 演算子を後置する
通常の中置記法(A + B のような表記)では演算子はオペランドの間にありますが、逆ポーランド表記では演算子がオペランドの後ろに置かれます。たとえば、「A + B」は逆ポーランド表記で「A B +」となります。 - カッコが不要
演算の優先順位を表すためにカッコを使う必要がありません。逆ポーランド表記では、演算子の順序が自動的に演算の順番を定義します。たとえば、通常の式「A + B × C」はカッコを使わないと優先順位が分かりにくいですが、逆ポーランド表記では「A B C × +」と表現することで、まず「B × C」が計算され、その結果に「A」が加えられることが明確になります。 - スタックを使用した計算
逆ポーランド表記の計算では、スタックというデータ構造を使ってオペランドを順次積み上げ、演算子が現れたらスタックの上にあるオペランドを取り出して計算し、その結果を再びスタックに戻すという方法を取ります。このため、式の評価が非常に効率的に行えます。
具体例
通常の式「(5 + 2) × 3」を逆ポーランド表記に変換する手順を見てみましょう。
- 中置記法(通常の式):(5 + 2) × 3
- 逆ポーランド表記:
- まず「5 + 2」を表すには、逆ポーランド表記で「5 2 +」となります。
- 次に、その結果に「× 3」を掛けるので、「5 2 + 3 ×」となります。
計算の手順(スタックを使った計算)
- 数字「5」をスタックに入れます。
- 数字「2」をスタックに入れます。
- 演算子「+」が来たので、スタックから「5」と「2」を取り出して加算し、その結果「7」をスタックに戻す。
- 数字「3」をスタックに入れます。
- 演算子「×」が来たので、スタックから「7」と「3」を取り出して掛け算し、最終結果「21」を得ます。
逆ポーランド表記の利点
- カッコが不要:式の優先順位や構造がカッコなしでも一意に決まるため、複雑な式の表現が簡潔になる。
- 評価が簡単:スタックを使って1回のスキャンで計算できるため、コンピュータのアルゴリズムで効率的に扱える。
- 直感的な理解が不要:人間にはやや馴染みにくいかもしれませんが、機械的な計算手順として非常に適している。
逆ポーランド表記法の使用例
逆ポーランド表記法は、かつてプログラミング言語や電卓で多く使用されていました。たとえば、ヒューレット・パッカード(HP)の古い電卓は逆ポーランド表記法に基づいて動作しており、技術者や科学者に非常に人気がありました。
逆ポーランド表記法のまとめ
逆ポーランド表記法は、演算子をオペランドの後ろに定める数式表記法で、括弧を使わずに演算の優先順位を明確に表せます。この方式はスタックを用いた計算処理に適しており、プログラムや電卓で効率的に利用されます。通常の中置記法と比べ、式の解釈が簡素化されるのが特徴です。
ハッシュ関数
自然数をキーとするデータを、ハッシュ表を用いて管理する。キー x のハッシュ関数 h(x) を
h(x) = x mod n
とすると、任意のキーa と bが衝突する条件はどれか。ここで、n はハッシュ表の大きさであり、 x mod nは x を n で割った余りを表す。
ア a+b が n の倍数
イ a-b が n の倍数
ウ n が a+b の倍数
エ n が a-b の倍数
引用:情報処理安全確保支援士試験 令和6年 秋 午前Ⅰ問3
解答
イ
問題の解説
この問題では、ハッシュ関数が次のように定義されています:
h(x) = x mod n
ハッシュ関数で使用されるmod(剰余)は、データを一定範囲の値に変換するための操作です。具体的には、入力値をある固定値で割った余りを計算し、結果として得られる値をハッシュ値として使用します。この操作により、任意の大きさのデータを指定範囲内のインデックスや識別子にマッピングできます。特にハッシュテーブルでのデータ配置や検索において、効率的な衝突回避と均一な分布を実現するために重要な役割を果たします。適切なmodの選定は、ハッシュ関数の性能に大きく影響します。
ここで、任意のキー aとbが衝突する条件を求めます。衝突するということは、ハッシュ関数の結果が同じになる、つまり次の条件が成り立つということです。
h(a) = h(b)
この条件を具体的に表すと、以下の式になります。
a mod n = b mod n
これはつまり、aとbをそれぞれnで割った余りが同じになることを意味します。この条件を式で表すと、次のようになります・
a ≡ b(mod n)
これは「a と b の差が n の倍数である」ということです。すなわち、
a – b = k * n(k は 整数)
したがって、a – bが n の倍数であるという条件が、キー a と b が衝突する条件です。
選択肢:
- ア a+bがnの倍数
- イ a-bがnの倍数 (正解)
- ウ nがa+bの倍数
- エ nがa-bの倍数
よって、正解は「イ:a-bがnの倍数」です。
ハッシュ関数
ハッシュ関数は、任意の長さの入力データ(キー)を固定長の値(ハッシュ値またはハッシュコード)に変換する関数です。ハッシュ関数は、特にコンピュータサイエンスや暗号技術で重要な役割を果たし、データの効率的な検索や検証に使用されます。以下に、ハッシュ関数の特徴や用途について説明します。
ハッシュ関数の特徴
- 固定長の出力
ハッシュ関数は、任意の長さの入力データを固定長のハッシュ値に変換します。たとえば、SHA-256というハッシュ関数は、どんな長さのデータを入力しても常に256ビットのハッシュ値を出力します。 - 同じ入力には同じ出力
同じ入力データをハッシュ関数に渡すと、常に同じハッシュ値が返されます。これにより、ハッシュ値を使ってデータの整合性を確認したり、同じデータかどうかを高速に比較できます。 - 効率性
ハッシュ関数は高速に計算できる必要があります。大量のデータや頻繁なアクセスがある場合でも、ハッシュ関数は迅速に結果を返すことが求められます。 - ハッシュ値の分散性
入力データがわずかに異なる場合でも、ハッシュ関数は大きく異なるハッシュ値を生成するように設計されています。これにより、ハッシュテーブルなどのデータ構造でデータが均等に分散され、効率的なデータ検索が可能になります。 - 衝突の可能性
入力データが異なるにもかかわらず、同じハッシュ値が生成されることを「衝突」といいます。理想的には、衝突が発生する確率は非常に低く、可能な限り避けられるべきです。ただし、有限のハッシュ値を持つハッシュ関数では、入力の数が多くなると衝突は理論上避けられません。
ハッシュ関数のまとめ
ハッシュ関数は、データを効率的に管理・検証するために欠かせない技術です。ハッシュテーブルによるデータ検索、データ整合性の検証、暗号化技術など、さまざまな分野で重要な役割を果たしており、特に大規模なデータ処理においてその威力を発揮します。
実行メモリアクセス時間
キャッシュメモリのアクセス時間が主記憶のアクセス時間の 1/30 で、ヒット率が95%のとき、実行メモリアクセス時間は、主記憶のアクセス時間の約何倍になるか。
ア 0.03
イ 0.08
ウ 0.37
エ 0.95
引用:情報処理安全確保支援士試験 令和6年 秋 午前Ⅰ問4
解答
イ
問題の解説
この問題では、キャッシュメモリと主記憶のアクセス時間、およびキャッシュのヒット率を使って、実行メモリアクセス時間(全体の平均アクセス時間)を求めます。
問題の条件
- キャッシュメモリのアクセス時間は主記憶のアクセス時間の 1/30。
- キャッシュのヒット率は 95%。
まず、次の記号を定義します。
- Tc:キャッシュメモリのアクセス時間
- Tm:主記憶のアクセス時間
- ヒット率:キャッシュメモリでデータが見つかる確率(95% = 0.95)
- ミス率:キャッシュメモリでデータが見つからない確率(5% = 0.05)
実行メモリアクセス時間の平均は、以下の式で計算されます。
実行メモリアクセス時間の計算式
実行メモリアクセス時間Tavgは、キャッシュメモリにヒットする場合とミスする場合を考慮して次のように表されます。
Tavg = (ヒット率)× Tc + (ミス率) × (Tc + Tm)
各値を式に代入
- キャッシュメモリのアクセス時間は主記憶の1/30なので、Tc = Tm/30。
- ヒット率 = 0.95
- ミス率 = 0.05
この情報を式に代入します。

まず、ヒット時の計算を行います。
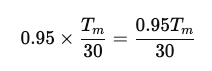
次に、ミス時の計算です。
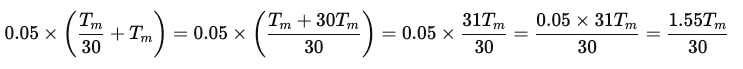
これらを合計すると、実行メモリアクセス時間は以下のようになります。
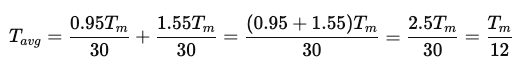
したがって、実行メモリアクセス時間は主記憶のアクセス時間の1/12(0.08333…)です。
選択肢の中で最も近いものは
- ア 0.03
- イ 0.08
- ウ 0.37
- エ 0.95
正解は「イ:0.08」です。
実行メモリアクセス時間
実行メモリアクセス時間(Effective Memory Access Time, EMAT)は、コンピュータのメモリアクセスの平均時間を指し、主記憶(メインメモリ)とキャッシュメモリがあるシステムにおいて、メモリにアクセスする際の効率を表す重要な指標です。特に、キャッシュメモリの存在を考慮した場合に、データのアクセスがキャッシュでヒットするか、ミスして主記憶にアクセスするかによってアクセス時間が異なるため、これを平均して求めたものが実行メモリアクセス時間となります。
実行メモリアクセス時間の計算
実行メモリアクセス時間は、キャッシュヒットとキャッシュミスの両方のケースを考慮して計算されます。基本的な考え方は以下の通りです:
- キャッシュヒット:キャッシュメモリに必要なデータが見つかった場合(ヒット)、キャッシュのアクセス時間のみで済むため、メモリアクセスが非常に高速になります。
- キャッシュミス:キャッシュメモリに必要なデータがない場合(ミス)、主記憶(メインメモリ)までアクセスしなければならないため、全体的なアクセス時間が遅くなります。
実行メモリアクセス時間は、これらの2つのケースの時間をヒット率とミス率を使って加重平均を取ることで計算されます。
実行メモリアクセス時間の計算式
一般的に、実行メモリアクセス時間(Tavg)は以下のように表されます。
Tavg = (ヒット率) × (キャッシュメモリのアクセス時間) + (ミス率) × (キャッシュメモリのアクセス時間 + 主記憶のアクセス時間)
ここで使用している各用語の説明は以下になります。
- ヒット率:キャッシュヒットの割合(キャッシュメモリでデータが見つかる確率)
- ミス率:キャッシュミスの割合(キャッシュメモリでデータが見つからない確率)
- キャッシュメモリのアクセス時間:キャッシュにデータがある場合のアクセス時間
- 主記憶のアクセス時間:キャッシュにデータがない場合、主記憶にアクセスする時間
実行メモリアクセス時間の重要性
- パフォーマンスの指標:実行メモリアクセス時間は、コンピュータシステムのメモリアクセス効率を評価する重要な指標です。特にキャッシュメモリの有効性(ヒット率やミス率)がシステム全体のパフォーマンスに与える影響を定量的に示します。
- キャッシュの設計:キャッシュメモリのサイズやキャッシュヒット率、主記憶のアクセス時間のバランスを取る際に、実行メモリアクセス時間を最小化することが目標となります。
- システムの高速化:実行メモリアクセス時間を短縮するために、キャッシュヒット率を向上させたり、キャッシュメモリを高速化する技術が開発されています。
実行メモリアクセス時間のまとめ
実行メモリアクセス時間は、コンピュータがメモリにアクセスする際の平均時間を表します。キャッシュメモリと主記憶の両方を考慮し、データがキャッシュに見つかる確率(ヒット率)によってアクセス時間が変化するため、システムのパフォーマンスに大きく影響します。実行メモリアクセス時間を短縮するためには、キャッシュヒット率の向上やキャッシュメモリの高速化などが重要です。
Webアプリケーションサーバの信頼性
Webアプリケーションサーバの信頼性に関する記述のうち、適切なものはどれか。
ア コールドスタンバイ構成で稼働しているサーバに障害が発生した場合、サービスは中断しないが、トランザクションは継続できない。
イ コールドスタンバイ構成で稼働しているサーバに障害が発生した場合、サービスは中断するが、トランザクションは継続できる。
ウ セッションを共有しないクラスタ構成で1台のサーバに障害が発生した場合、サービスは継続できないが、トランザクションは継続できる。
エ セッションを共有するクラスと構成で1台のサーバに障害が発生した場合、サービス及びトランザクションは継続できる。
引用:情報処理安全確保支援士試験 令和6年 秋 午前Ⅰ問5
解答
エ
問題の解説
この問題では、Webアプリケーションサーバの信頼性に関する構成と動作について問われています。それぞれの選択肢に対して解説を行い、適切なものを選びます。
選択肢ごとの解説
ア コールドスタンバイ構成で稼働しているサーバに障害発生した場合、サービスは中断しないが、トランザクションは継続できない。
誤り
<解説>
コールドスタンバイ構成とは、予備サーバ(スタンバイサーバ)が待機していて、現用サーバに障害が発生した際に手動または自動で予備サーバに切り替える方式です。コールドスタンバイでは、障害発生時に予備サーバが起動するまでの間、サービスは中断します。したがって、「サービスは中断しない」は誤りです。
イ コールドスタンバイ構成で稼働しているサーバに障害が発生した場合、サービスを中断するが、トランザクションは継続できる。
誤り
<解説>
コールドスタンバイでは、障害発生時に予備サーバが起動するため、サービスは一時的に中断します。また、一般的にコールドスタンバイ構成では、トランザクションの状態が引き継がれることはないため、トランザクションは継続できません。このため「トランザクションは継続できる」という部分が誤りです。
ウ セッションを共有しないクラスタ構成で1台のサーバに障害が発生した場合、サービスは継続できないが、トランザクションは継続できる。
誤り
<解説>
セッションを共有しないクラスタ構成では、セッション情報が個々のサーバに依存しているため、1台のサーバが障害を起こすとそのサーバ上のセッションは失われます。したがって、トランザクションも継続できません。また、他のサーバが正常に動作している場合、サービス自体はクラスタ全体で継続されるため、「サービスは継続できない」も誤りです。
エ セッションを共有するクラスタ構成で1台のサーバに障害が発生した場合、サービス及びトランザクションは継続できる。
正しい
<解説>
セッションを共有するクラスタ構成では、セッション情報やトランザクションの状態がクラスタ全体で管理されるため、1台のサーバに障害が発生しても他のサーバがその役割を引き継ぐことができます。これにより、サービスが中断することなく、トランザクションも継続することが可能です。この記述は正しいです。
Webアプリケーションサーバにおける信頼性のまとめ
Webアプリケーションサーバの信頼性を高めるためには、セッションの共有、負荷分散、フェイルオーバーなどの仕組みを組み合わせることが重要です。選択肢の中で、これらの特徴を最もよく表しているのがエの「セッションを共有するクラスタ構成」です。
まとめ
今回は、下記について説明しました。
- AIにおける教師あり学習での交差検証
- 逆ポーランド表記法
- ハッシュ関数
- 実行メモリアクセス時間
- Webアプリケーションサーバの信頼性
今回は、令和6年度秋期午前Ⅰ共通問題の問1から問5で出題された用語について説明しました。次回は、問6から問10について説明します。
これからも、Macのシステムエンジニアとして、日々、習得した知識や経験を発信していきますので、是非、ブックマーク登録してくれると嬉しいです!
それでは、次回のブログで!


